1135 Is It A Red-Black Tree (30 分)

2019-05-09

1135 Is It A Red-Black Tree (30 分)

There is a kind of balanced binary search tree named red-black tree in the data structure. It has the following 5 properties:

(1) Every node is either red or black.
(2) The root is black.
(3) Every leaf (NULL) is black.
(4) If a node is red, then both its children are black.
(5) For each node, all simple paths from the node to descendant leaves contain the same number of black nodes.

For example, the tree in Figure 1 is a red-black tree, while the ones in Figure 2 and 3 are not.


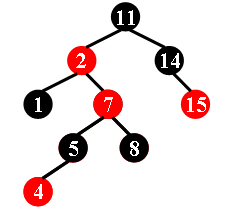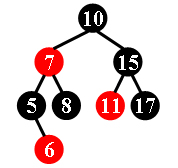Figure 1	Figure 2	Figure 3

For each given binary search tree, you are supposed to tell if it is a legal red-black tree.

Input Specification:

Each input file contains several test cases. The first line gives a positive integer K (≤30) which is the total number of cases. For each case, the first line gives a positive integer N (≤30), the total number of nodes in the binary tree. The second line gives the preorder traversal sequence of the tree. While all the keys in a tree are positive integers, we use negative signs to represent red nodes. All the numbers in a line are separated by a space. The sample input cases correspond to the trees shown in Figure 1, 2 and 3.

Output Specification:

For each test case, print in a line “Yes” if the given tree is a red-black tree, or “No” if not.

Sample Input:

3
9
7 -2 1 5 -4 -11 8 14 -15
9
11 -2 1 -7 5 -4 8 14 -15
8
10 -7 5 -6 8 15 -11 17

Sample Output:

1
2
3

Yes
No
No

作者: CHEN, Yue

单位: 浙江大学

时间限制: 400 ms

内存限制: 64 MB

代码长度限制: 16 KB

题目大意

给出一棵二叉树的前序遍历，要求判断是否为红黑树。红黑树的规则如下：

所有结点非红即黑
根结点为黑色
叶子结点（NULL结点）为黑色。
红色结点的孩子都是黑色
对于每一个结点，其到叶子结点的所有路径含有相同数目的黑色结点

分析

首先建立出树。使用map标记为红色的结点。判断是否为红黑树，主要判断2、4、5性质。首先判断根结点是否黑色。然后从根结点dfs，遇到红结点判断其孩子颜色是否全黑。然后判断左右子树上黑结点数是否相同。

代码

#include <iostream>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;
int k,n,is;
map<int,int>neg;
vector<int> pre,in;
struct node{
    int v;
    node* left;
    node* right;
};
node* buildtree(int pres,int pree,int ins,int ine){
    if(pres>=pree||ins>=ine)
        return nullptr;
    int cur=pre[pres];
    node* root=new node;
    int i=ins;
    while(i<ine&&in[i]!=cur)i++;
    root->v=cur;
    root->left=buildtree(pres+1, pres+i-ins+1, ins, i);
    root->right=buildtree(pres+i-ins+1, pree, i+1, ine);
    return root;
}
int dfs(node* root){//返回黑色结点的数量
    if(is==0)//已经不是红黑树，返回
        return 0;
    if(root==nullptr)
        return 1;//null结点为黑色
    if(neg[root->v]==1){//判断红色结点孩子颜色
        if(root->left&&neg[root->left->v]==1)
            is=0;
        if(root->right&&neg[root->right->v]==1)
            is=0;
    }
    int leftb=dfs(root->left);
    int rightb=dfs(root->right);
    if(leftb!=rightb)//判断左右路径黑结点数是否相同
        is=0;
    if(neg[root->v]==0)
        return leftb+1;//此结点为黑色，黑结点数量+1
    else
        return leftb;
}
int main() {
    cin>>k;
    node* root;
    while(k--){
        pre.clear();
        in.clear();
        neg.clear();
        cin>>n;
        int t;
        for(int i=0;i<n;i++){
            cin>>t;
            if(t<0){
                t=-t;
                neg[t]=1;
            }
            pre.push_back(t);
        }
        in=pre;
        sort(in.begin(),in.end());
        root=buildtree(0,n,0,n);
        //is为全局变量，标记是否为红黑树
        is=1;
        if(neg[root->v]==1)
            is=0;
        if(is)
            dfs(root);
        if(is)
            cout<<"Yes"<<endl;
        else
            cout<<"No"<<endl;
    }
    return 0;
}